Tugas 4 Limit Fungsi

Rumus Limit Fungsi

Dalam dunia matematika, Limit biasa di tuiskan sebagai berikut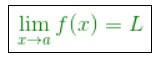

Keterangan :

Apabila x mendekati a tetapi x tidak sama dengan a maka f(x) mendekati L
Pendekatan x ke a bisa dilihat dari dua sisi yaitu pada sisi kiri dan sisi kanan ataupun dengan kata lain x bisa mendekati dari arah kiri dan arah kanan hingga menghasilkan limit kiri serta limit kanan

Sifat Fungsi Limit Aljabar

Jika n adalah bilangan bulat positif, k konstanta, f dan g ialah fungsi yang mempunyai limit di c, maka sifat-sifat yang berlaku yaitu: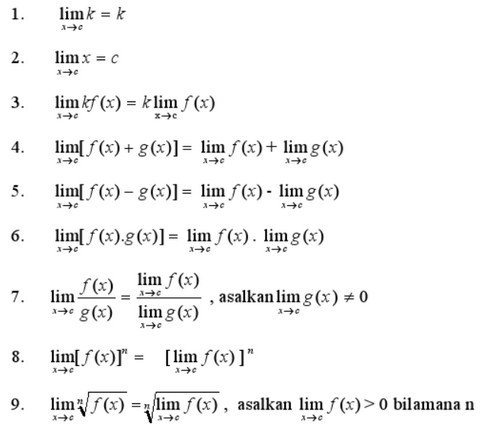

Macam-Macam Metode Limit Aljabar

metode subitusi
metode pemfaktoran
metode membagi dengan pangkat tertinggi penyebut
metode mengalikan dengan faktor sekawan

1. Metode Subsitusi

Metode subsitusi hanya mengganti peubah yang mendekati nilai tertentu dengan fungsi aljabarnya
Contoh

Jadi nilai fungsi limit baljabar adalah

2. Metode Pemfaktoran

Metode pemfaktoran dipakai jika metode subsitusi yang menghasilkan nilai limit tidak terdefinisikan
Contoh :

Metode pemfaktoran dilakukan dengan menentukan faktor persekutuan antara pembilang dan penyebutnya.

Dengan kaitanya pada bentuk limit kedua ada beberapa metode dalam menentukan nilai limit fungsi aljabar yaitu metode membagi dengan pangkat tertinggi penyebut dan metode mengalikan dengan faktor sekawan

3. Metode Membagi Pangkat Tertinggi Penyebut

Contoh 1 :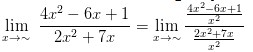

Tentukanlah nilai limit fungsi aljabar dari

Besar pangkat pembilang dan penyebut dalam soal yaitu 2, jadi,

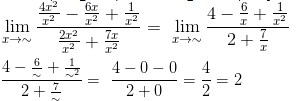
Maka, nilailimit fungsi aljabar tersebut adalah

Contoh 2 :
Tentukan nilai limit fungsi aljabar dari

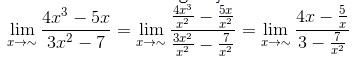
Besar pangkat pembilang dan penyebut dalam soal yaitu 3,
jadi,

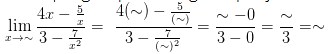
Maka, nilai dari limit fungsi aljabar tersebut yaitu

4. Metode Mengalikan Dengan Faktor Sekawan

Contoh soal :
Tentukan nilai limit dari

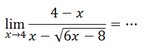
Langkah pertama yang perlu dilakukan untuk menentukan nilai suatu limit adalah dengan mensubtitusikan x = c ke f(x), hingga dalam kasus ini substitusikan
x=4 ke

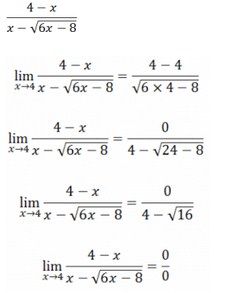
Setelah disubstitusikan ternyata nilai limit tidak terdefinisi atau merupakan bentuk tak tentu

Maka itu untuk menentukan nilai suatu limit wajib menggunakan metode lain. Jika diperhatikan, pada f (x) ada bentuk akar yaitu

hingga metode perkalian dengan akar sekawaran bisa dilakukan pada kasus seperti ini.

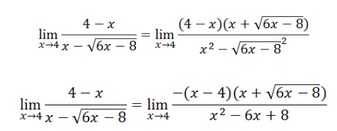
Bentuk

bisa difaktorkan jadi

Maka, nilai limit fungsi aljabar tersebut ialah -4

Limit Fungsi Trigonometri

Limit juga dapat digunakan pada fungsi trigonometria Penyelesaiannya sama dengan fungsi limit aljabar. Namun, agar mengerti penjalasan selanjutnya harus mengerti terlebih dahulu konsep dari trigonometri. Penyelesaian dalam limit fungsi ini dalam trigonometri bisa dilakukan dengan melakukan perubahan-perubahan bentuk sinus, cosinus, dan tangen.
Ada tiga bentuk umum dalam limit fungsi trigonometri, yaitu bentuk :

1. Bentuk 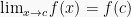$\lim_{x\to c}f(x) = f(c)$

Pada bentuk ini, limit dari fungsi trigonometri f(x) merupakan hasil dari substitusi nilai c ke dalam x dari trigonometri. Contoh :

No.	CONTOH	NILAI LIMIT
1	$\lim \limits_{x\to ^\pi/_4} \sin 2x$	$\sin \frac{\pi}{2}$
2	$\lim \limits_{x\to \pi} \cos \frac{1}{2}x$	$cos\frac{1}{2}\pi$
3	$\lim \limits_{x\to ^\pi/_2} \tan x$	$\tan\frac{\pi}{2}$

Jika c = 0, maka rumus limit-limit trigonometrinya adalah sebagai berikut :

$\lim \limits_{x\to 0} \sin x = 0$
$\lim \limits_{x\to 0} \cos x = 1$
$\lim \limits_{x\to 0} \cos x = 0$

2. Bentuk $\lim_{x\to c}\frac{f(x)}{g(x)}$

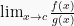
Pada bentuk ini, limit diperoleh dari perbandingan 2 trigonometri berbeda. Kedua trigonometri tersebut jika langsung disubstitusi dengan nilai c menghasilkan f(c) = 0 dan g(c) = 0. Sehingga, nilai limit trigonometri tersebut menjadi bilangan tak tentu $\frac{0}{0}$ . Penyelesaiannya sama dengan limit fungsi aljabar yaitu pemfaktoran. Contoh bentuk ini yaitu:

$\lim \limits_{x\to ^\pi/_2}\frac{\sin 2x}{cosx} = \frac{2 \cos x \sin x}{cosx} = 2 \sin x = 2 \sin \frac{\pi}{2} = 2$

3. Bentuk $\lim_{x\to 0}\frac{f(x)}{g(x)}$

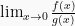
Pada bentuk ini, limit diperoleh dari perbandingan antara trigonometri dan fungsi aljabar. Jika disubstitusikan langsung akan menghaslikan bilangan tak tentu. Pada bentuk ini dikerjakan dengan konsep turunan Bentuk rumus dasar limit ini adalah:

$\lim \limits_{x\to 0}\frac{\sin x}{x} = \lim_{x\to 0}\frac{x}{\sin x} = 1$
$\lim \limits_{x\to 0}\frac{x}{\cos x} = 0$
$\lim \limits_{x\to 0}\frac{\cos x}{x} = \infty$
$\lim \limits_{x\to 0}\frac{\tan x}{x} = \lim_{x\to}\frac{x}{\tan x} = 1$

Berdasarkan rumus dasar diataas, jika dikembangkan menjadi rumus-rumus berikut:

$\lim \limits_{x\to 0}\frac{\sin ax}{bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{ax}{\sin bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{ax}{\cos bx} = 0$
$\lim \limits_{x\to 0}\frac{\cos ax}{bx} = \infty$
$\lim \limits_{x\to 0}\frac{\tan ax}{bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{ax}{\tan bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{\sin ax}{\tan bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{\tan ax}{\sin bx} = \frac{a}{b}$

Contoh Soal Limit Fungsi dan Pembahasan

Contoh Soal Limit 1

Tentukanlah nilai dari $\lim_{x\to 2}(\frac{6-x}{x^2-4} - \frac{1}{x-2})$

Pembahasan 1 :

$\lim \limits_{x\to 2}(\frac{6-x}{x^2} - \frac{1}{x-2}) = \lim \limits_{x\to 2}(\frac{6-x}{x^2-4} - \frac{x+2}{(x-2)(x+2)})$ $= \lim \limits_{x\to 2}\frac{(6-x) - (x+2)}{(x-2)(x+2)}$

$=\lim \limits_{x\to 2}\frac{4-2x}{(x-2)(x+2)} = \lim \limits_{x\to 2}\frac{-2(x-2)}{(x-2)(x+2)}$ $= \lim \limits_{x\to 2}\frac{-2}{(x+2)}$

$=-\frac{2}{4} = -\frac{1}{2}$

Contoh Soal Limit 2

Tentukanlah nilai dari $\lim \limits_{x\to \infty}(\frac{\sqrt{4x+x^2} - \sqrt{2+x^2}}{3x})$

Pembahasan 2:

$\lim \limits_{x\to \infty}(\frac{\sqrt{4x+x^2}-\sqrt{2+x^2}}{3x}) = \lim_{x\to \infty}(\frac{\sqrt{\frac{4}{x^2}+\frac{x^2}{x^2}}-\sqrt{\frac{2}{x^2}+\frac{x^2}{x^2}}}{\frac{3x}{x}})$ $= \lim_{x\to \infty}(\frac{\sqrt{\frac{4}{x^2}+1}-\sqrt{\frac{2}{x^2}+1}}{3})$

$=(\frac{1-1}{3}) = \frac{0}{3} = 0$

Contoh Soal Limit 3

Tentukanlah nilai dari $\lim \limits_{x\to 0}(\frac{x^2+ \sin x \tan x}{1- \cos 2x})$

$\lim \limits_{x\to 0}(\frac{x^2+ \sin x \tan x}{1- \cos 2x}) = \lim \limits_{x\to 0}(\frac{x^2+ \sin x \tan x}{2sin^2x})$ $= \lim \limits_{x\to 0}(\frac{x^2}{2 \sin^2x}+\frac{\sin x \tan x}{2sin^2x})$

$= \lim \limits_{x\to 0}(\frac{x^2}{2sin^2x}+\frac{\sin x \tan x}{2 \sin^2x})$ $= \lim \limits_{x\to 0}(\frac{x^2}{2 \sin^2x}+\frac{\tan x}{2 \sin x})$

Tugas Matematika

Cari Blog Ini