Fungsi Implisit
Penyelesaian:
Penyelesaian:




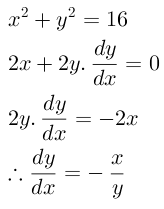

[penyelesaian]
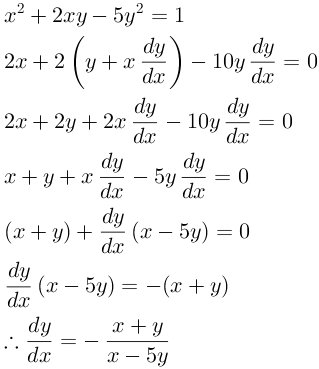
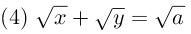
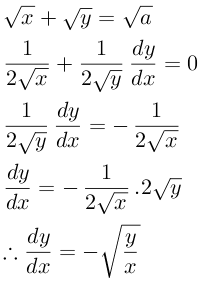

[Penyelesaian]

3x2-6xy-3x2dydx+2ydydx=0
dydx(-3x2+2y)=-3x2+6xy
dydx=-3x2+6xy-3x2+2y
Fungsi implisit adalah fungsi yang terdiri
dari dua atau lebih variabel yakni variabel bebas dan variabel tak
bebas, yang berada dalam satu ruas dan tidak bisa dipisahkan pada ruas
yang berbeda.
Menurunkan fungsi implisit, tak jauh beda
dengan menurunkan fungsi variabel tunggal, yakni dengan menggunakan
notasi Leibniz (dy/dx). Berikut ini, hal yang harus dipahami dalam
menurunkan fungsi implisit khususnya yang memiliki dua variabel (x dan
y).
Untuk lebih memahami, perhatikan 5 pembahasan soal di bawah:
1. Turunan pertama dari fungsi implisit (x + 2y)^8 adalah…
2. Nyatakan dalam dy/dx, turunan fungsi implisit x³ + 5 ln xy – 3xy^-1 = -4Penyelesaian:

- Jika fungsi implisit mengandung unsur trigonometri.
3. Turunan pertama dari fungsi implisit sin xy + xy² + x²y = 1 adalah…
- Jika fungsi implisit berbentuk fungsi pembagian.
4. Turunan pertama fungsi implisit f(x,y) = (y – x²)/(y² – x) adalah…
- Jika mencari titik kritis dari fungsi implisit.
Penyelesaian:


Definisi Turunan Fungsi Implisit yaitu
fungsi yang memuat dua variabel atau lebih, variabel-variabel
tersebut terdiri dari variabel bebas dan variabel tidak bebas, biasanya
variabel-variabel tersebut dinyatakan dalam x dan y dimana variabel x
dan y terletak didalam satu ruas sehingga tidak dapat dipisahkan menjadi
ruas yang berbeda (baca : ruas kiri dan ruas kanan) seperti halnya
fungsi eksplisit.
|
Turunan Fungsi Implisit Serta bentuk umum nya
Secara umum bentuk turunan fungsi implisit adalah
f(x,y) = 0, mencari turunan fungsi implisit sama dengan mencari solusi
bentuk umumnya dan prinsipnya tidak jauh berbeda dengan mencari turunan fungsi biasa.
Untuk lebih jelasnya Perhatikan contoh-contoh soal dibawah ini, bagaimana mencari turunan fungsi implisit.
Contoh :
Tentukan 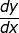 dari setiap fungsi Implisit dibawah ini!
dari setiap fungsi Implisit dibawah ini!
[Penyelesaian]
Turunkanlah kedua ruas terhadap x,
[Penyelesaian]
Turunkanlah kedua ruas terhadap x,
[penyelesaian]
Turunkanlah kedua ruas terhadap x
[Penyelesaian]
Turunkanlah kedua ruas terhadap x
[Penyelesaian]
Turunkanlah kedua ruas terhadap x
Beberapa kasus dapat diselesaikan dengan 2 cara yaitu:
Cara I :
x3-3x2y+y2=03x2-6xy-3x2dydx+2ydydx=0
dydx(-3x2+2y)=-3x2+6xy
dydx=-3x2+6xy-3x2+2y
Cara II:
x3-3x2y+y2=0
3x2dx-6xy dx-3x2dy+2y
dy=03x2-6xy-3x2dydx+2ydydx=0:dx
dydx(-3x2+2y)=-3x2+6xy
dydx=-3x2+6xy-3x2+2y




Komentar
Posting Komentar